The Recurrence Relation

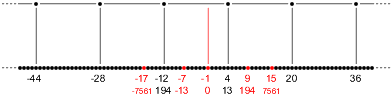
Let's pause for a moment and regroup. Here's a picture that shows the key features.

At the top we have the bidirectional chain values. At the bottom we have the bidirectional upper denominators q_n. The center point is shown, as are the positions where u, v, and w appear. Positions that aren't aligned with the chain are shown in red. Also remember that the alternating signs make q_n negative when n is negative and odd.

Now, the pièce de résistance! Suppose we have any purely repeating expansion of length L. For reference, let's compute the numerators and denominators for the first iteration only, as in Group Elements and Matrices but without the “z” at the end.

		a0	a1	…	aL−2	aL−1
p−2 = 0	p−1 = 1	p0	p1	…	pL−2	pL−1
q−2 = 1	q−1 = 0	q0	q1	…	qL−2	qL−1

Let's also recall the equations that define the numerators and denominators.

p_n+1 = a_n+1p_n + p_n−1
q_n+1 = a_n+1q_n + q_n−1

I said “equations”, but clearly there's really only one equation. The solutions are different because the initial conditions are different: (0,1) for the numerators and (1,0) for the denominators. Now, suppose we have another solution r_n. The equation is linear, so if we multiply p_n by the constant r₋₁, multiply q_n by the constant r₋₂, and add, we get a solution with initial conditions (r₋₂,r₋₁). Since r_n has the same initial conditions, the two must be equal for all n.

r_n = p_n r₋₁ + q_n r₋₂

In particular, here are the equations for the last two columns of the table.

rL−1 = pL−1 r−1 + qL−1 r−2	(1)
rL−2 = pL−2 r−1 + qL−2 r−2	(2)

In the same way, we can construct a solution with initial conditions (r_L−2,r_L−1). Since a_n+L = a_n, the translated solution r_n+L is still a solution, and it has the same initial conditions, so again the two must be equal for all n.

r_n+L = p_n r_L−1 + q_n r_L−2

In particular, here are the equations for the last two columns of the table.

r2L−1 = pL−1 rL−1 + qL−1 rL−2	(3)
r2L−2 = pL−2 rL−1 + qL−2 rL−2	(4)

That gives us four equations in six unknowns. Let's do some easy algebra.

1. Start with equation (3).
2. Eliminate r_2L−2 by simply throwing out equation (4).
3. Use equation (2) to eliminate r_L−2.
4. Use equation (1) to eliminate r₋₂. This is easy because r₋₂ only appears in the term q_L−1 q_L−2 r₋₂ = q_L−2 (q_L−1 r₋₂).

That leaves us with one equation in three unknowns.

r_2L−1 − (p_L−1 + q_L−2) r_L−1 + (p_L−1 q_L−2 − p_L−2 q_L−1) r₋₁ = 0

Next, let E be the associated matrix of the group element that adds the prefix that we've been talking about.

pL−1	pL−2
qL−1	qL−2

With that, we can make our one equation more compact.

r_2L−1 − (tr E) r_L−1 + (det E) r₋₁ = 0

We can generalize that nice result in two ways, but first we need one more definition.

Let s_k be the bidirectional subsequence of r_n where n is congruent to k mod L.

Technically we ought to define the allowed values of k and also include a second subscript n so that we can refer to the individual terms of s_k, but that's all very tedious.

So, the nice result relates three consecutive terms of s₋₁, or s_L−1 if you prefer. However, just as we can translate solutions by L, we can translate them by any multiple of L, therefore the nice result applies to any three consecutive terms of s₋₁! In other words, the whole subsequence s₋₁ obeys a recurrence relation with the following characteristic polynomial.

x² − (tr E) x + (det E)

That's the first generalization.

What happens if we translate a solution by an amount k that's not a multiple of L?

1. We still get a solution, but it's a solution to a different equation, or rather a solution to the same equation with different coefficients a_n. To be precise, the translated solution r_n+k has coefficients a_n+k that describe the rotation of the original expansion that starts with a_k.
2. So, the subsequence s₋₁ of the translated solution obeys a recurrence relation with the same characteristic polynomial as the subsequence s₋₁ of the original solution except that the matrix E comes from a rotation of the original expansion. That's a mouthful, so let's just say “obeys a rotation” instead.
3. The subsequence s₋₁ of the translated solution is the same as the subsequence s_k−1 of the original solution (for example, both contain r_k−1), so that too obeys a rotation.
4. Since I count the original expansion as a rotation, the subsequence s₋₁ of the original solution also obeys a rotation.

So, putting the pieces together, we can say that every subsequence s_k of the original solution obeys a rotation. That's the second generalization.

What do the different matrices E look like? They do have to be different from one another since we can go backward from matrix to expansion, and the expansions are different. Remember the prefix function P from The Random Thoughts? We can use that to write the original matrix E as a product.

E = P(a₀) P(a₁) … P(a_L−2) P(a_L−1)

The other matrices E look the same except that the factors are rotated. Now, there are some things we can say about products of matrices.

• The determinant of a product is the product of the determinants. So, since det P(a) = −1, we must have det E = (−1)^L … but we already knew that from Group Elements and Matrices.
• The trace of a product is invariant under rotation. The reason is easy to understand: if you write out the row and column indices, then the matrix multiplications connect adjacent factors and the trace closes the loop.

As a result, the different matrices E all have the same determinant and the same trace, which means that the different subsequences s_k all have the same characteristic polynomial and obey the same recurrence relation. That's the true second generalization.

Finally, let's specialize in two ways. Don't worry, it'll be quick! First, take the arbitrary purely repeating expansion to be expansion(u), so that L becomes L(u) and E becomes E(u). Second, take the arbitrary solution r_n to be the denominators q_n. Then, we already know that det E(u) = 1 and tr E(u) = 3u, so the subsequences s_k of the denominators all obey a recurrence relation with characteristic polynomial x² − 3ux + 1 … just like the chain values! Bang! Stay tuned, we'll continue from that point after a quick story break.

In the essay Continued Fractions, I mentioned that I first heard about continued fractions in high school. Here's how that happened. There was a series of educational books called the New Mathematical Library. My high school math teacher had several of them, and loaned me this one, and probably one or two others at other times.

[Olds] Continued Fractions

I read some of it, enough to get the basic idea, but I doubt I got more than a third of the way through.

In February 2022, when the current madness started, it occurred to me that it would be fun to see that old book again, and so on February 25, the day I started writing Approximation Quality, I ordered a copy. (A used copy, because the book's out of print.) However, as with [Aigner], I decided not to read it until I was done writing.

In September 2022, when I declared the essays essentially done, as a reward I gave myself permission to read [Olds]. I could see from the table of contents that the book didn't discuss the Markov constant, so I knew it wouldn't influence the random thoughts. So, I was quite surprised to find the following problem on p. 81, about halfway through. (I reformatted the definition of x.)

Verify, by giving the positive integers a and b particular values, and by selecting particular convergents p_n−2/q_n−2, p_n/q_n, p_n+2/q_n+2, that if

x = [0,a,b],

then

p_n+2 − (ab + 2)p_n + p_n−2 = 0.

That one hint led to all the theory in this essay. I had thought it was just some kind of bizarre accident that denominators contained chains, an intractable problem, but if every repeating expansion had a recurrence relation that applied to every subsequence, well, that sounded pretty tractable. And it was!

I did have to stop reading [Olds], though.