Sketch of a Proof

Let me show you one more interesting thing about the large example. Remember how in Symmetries the flips from the solution (u,v,w) led to the solutions (u_v,u,w) and (u_w,u,v)? Here the actual numbers are u_v = 294685 and u_w = 4400489. But, we've seen those numbers before! Most recently they appeared as intermediate chain values in this table from Going Backward.

36		6684339842
20		294685
4		13
−12		194
−28		4400489
−44		99816291793

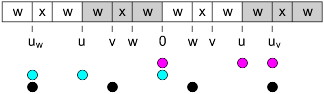
Here's a picture that shows everything that's going on.

The black dots point out that the intermediate chain values are equally spaced. The magenta and cyan dots point out that the heuristic pictures from Positions are compatible with the new equations.

expansion(uv)	= expansion(u) & expansion(w)
expansion(uw)	= expansion(u) & expansion(v)

The fact that u_v and u_w appear in the denominators for u suggests that we might be able to use induction over the tree of solutions to prove that the table of positions is correct. Let's give it a try! So, suppose that for the solution (u,v,w) we know that (1) the table of positions is correct and (2) the denominators have the expected triangle structure with the symmetrical part in the middle. Those things are actually not true for (1,1,1) and (2,1,1), but they are true for (5,2,1), so that will be the starting point of the induction. Here are those denominators, partly to help you check what I just said and partly to remind you what the triangle structure looks like. Note that the symmetrical part is empty.

0		1		2		1		2
1		1		1		2		2
2		2		1
						3		1
3		5		2		5		1

And here's the table of positions again for reference.

	lower		upper
w	L(w)	− 1	L(w)	− 1 − δ	6
v	L(v)	− 1 + δ	L(v)	− 1	10
u	L(u)	− 1	L(u)	− 1	16

What I want to do next is take those two tables, condense them as much as possible, and then use them to observe what happens when we make certain changes to the expansions. Here's the result, a little movie with five frames. Each frame contains two columns.

		11	2		11	2		2	2		11	2		11	2
		2	11			2		2	2		2	11		2	11
w		−1	−2		−1	−2		−2	−2		−1	−2		−1	−2
v		0	−1		0	−1		−1	−1		0	−1
u		−1	−1		−1	−1		−1	−1		0	−1		0	−1
uv						−2		−2	−2		−1	−1		−1	−1

The first frame shows the standard values for a solution with δ = +1. The first two rows show the contents of the top and bottom triangles. The rest is just the table of positions with the L(x) terms removed. In other words, it's a table of offsets.

In the second frame we shift our focus from u to u_v. Here I want to argue by example. If you look back at the table of denominators in the first part, you can see that u_v = 294685 appears in the upper denominators at position 20 with coefficient 2. Since L(u_v) = 22, the offset is −2, and that gives us all the information we need for the frame.

In fact, the offset for u_v is always equal to the offset for w. That's easy to prove, but sadly not easy to explain in prose, so here are some equations, even though it's overkill. On the one hand, u_v and w are consecutive chain values.

position(u_v) = position(w) + L(u)

On the other hand, the expansion lengths are related by the pattern.

L(u_v) = L(u) + L(w)

Subtracting the second equation from the first yields the desired result.

Now, the first problem we have is that u_v doesn't appear on the left side. In the third frame we fix that by simply copying the entire right side to the left. Now is a good time to explain that entries in bold are ones that have been overwritten (with the same value, in one case).

The second problem we have is that u_v is in the wrong position on both sides. In the fourth frame we fix that by lengthening the expansions. On the right side we perform a proper-improper conversion in the bottom triangle, which only changes the position of u_v. On the left side we perform a same-denominator conversion in the top triangle, which changes all the positions.

In the fifth frame we forget about v and are left with the standard values for a solution with δ = +1 … except that now the solution is (u_v,u,w)! For completeness, I should point out that that solution does in fact have δ = +1. We did a v-flip, so the number of w-flips hasn't changed, so δ(u_v) = δ(u). And that's the end of that case of the induction!

The w-flip case is similar.

		11	2		11	2		11	11		2	11		2	11
		2	11		11			11	11		11	2		11	2
w		−1	−2		−1	−2		−1	−1		−2	−1
v		0	−1		0	−1		0	0		−1	0		−1	0
u		−1	−1		−1	−1		−1	−1		−2	−1		−2	−1
uw					0			0	0		−1	−1		−1	−1

The first frame shows the standard values for a solution with δ = +1.

In the second frame we shift our focus from u to u_w. Consulting the table of denominators in the first part, we find that u_w = 4400489 appears in the lower denominators at position 26 (offset 0) with coefficient 1 and previous coefficient 1. Also, by the same argument as before, the offset for u_w is always equal to the offset for v.

In the third frame we copy the entire left side to the right.

In the fourth frame we shorten the expansions. On the right side we perform a proper-improper conversion in the bottom triangle, which only changes the position of u_w. On the left side we perform a same-denominator conversion in the top triangle, which changes all the positions.

And, in the fifth frame we forget about w and are left with the standard values for a solution with δ = −1, which of course is exactly what we want for the solution (u_w,u,v). We did a w-flip, so the number of w-flips has ticked up, so δ(u_w) = −δ(u).

The δ = −1 cases are so similar that I've got nothing to say. Here's the v-flip case.

		2	11		2	11		11	11		2	11		2	11
		11	2			11		11	11		11	2		11	2
w		−1	0		−1	0		0	0		−1	0		−1	0
v		−2	−1		−2	−1		−1	−1		−2	−1
u		−1	−1		−1	−1		−1	−1		−2	−1		−2	−1
uv						0		0	0		−1	−1		−1	−1

And here's the w-flip case.

		2	11		2	11		2	2		11	2		11	2
		11	2		2			2	2		2	11		2	11
w		−1	0		−1	0		−1	−1		0	−1
v		−2	−1		−2	−1		−2	−2		−1	−2		−1	−2
u		−1	−1		−1	−1		−1	−1		0	−1		0	−1
uw					−2			−2	−2		−1	−1		−1	−1

Two quick technical notes about the “lengthen” and “shorten” operations:

• If a denominator of interest is so small that it appears before the symmetrical part, then it's not obvious that it will change position as expected. We can use the table of denominators for u = 5, above, to investigate. The denominator 2 does change position as expected, but the denominator 1 appears on the left side twice. However, the one in the position 0 is never used, because columns that start with 11 never contain the necessary offset −2.
• To preserve the triangle structure, we must always lengthen and shorten diagonally opposite entries. But why are the entries always the bottom right and top left instead of the bottom left and top right? I don't think there's any real reason, that's just how it goes.

So, we've demonstrated that if the solution (u,v,w) satisfies two conditions, …

… (1) the table of positions is correct and (2) the denominators have the expected triangle structure with the symmetrical part in the middle.

… then in all cases the child solutions (u_v,u,w) and (u_w,u,v) satisfy the same two conditions. Why is that not a proof? There are two reasons.

The first reason is that we didn't really demonstrate everything we needed to. One input is missing, because in the second frame we don't know that the new denominator u_v or u_w appears with the appropriate coefficient(s), and one output is missing, because in the end we don't know that the new symmetrical part is actually symmetrical.

The second reason is that we implicitly made use of another condition. To know that u_v and u_w appear in the denominators, we need to know not just that v and w appear but also that the recurrence relation holds, and the recurrence relation only holds because the expansion is specifically expansion(u). So, we also need to demonstrate that the new expansions are expansion(u_v) and expansion(u_w), but I have no idea how to do that.

That's the end of the story of chains and denominators.