The Pattern

When I was gathering facts for these essays and trying to put them together into some kind of coherent structure, there were times when it was hard to find the structure, but the raw facts were always more or less available in [Hua] and on Wikipedia. But, when I reached the heart of the matter, the question of which numbers produce the beautiful pattern at M < 3 related to the Markov equation, I found that [Hua] and Wikipedia disagreed … and, according to my calculations, were both wrong.

Let me interrupt the story for a minute to give some details. [Hua] claims that the following numbers work, …

(1/2u) [ u + (2v/w) + root D ]

… but that formula fails at u = 29. And, Wikipedia (in [MC]) claims that the following numbers work, …

(1/2u) [ 2t − 3u + root D ]

… where t is the smallest positive integer such that t² + 1 is divisible by u, but that formula fails at u = 610 (t = 133). How do I know that those numbers don't produce the desired values of M? First, the expansions repeat, so computing M is a finite process, not an infinite one. I mentioned the reason in the essay Continued Fractions.

… the expansion repeats if and only if the original number was the root of a quadratic equation … technically, an irreducible quadratic with rational coefficients.

Second, the repeating parts of the expansions aren't all 1s and 2s, so computing M isn't even necessary.

Now, where was I? [Hua] and Wikipedia were both wrong, and I was frustrated. I supposed there was probably a correct formula somewhere, and I had some leads in the form of Wikipedia references, but I wasn't filled with joy at the prospect of spending hours at the university library digging around in math journals. Also, it wasn't the numbers that I wanted to know, it was the expansions, because I thought there might be a nice pattern there.

I'm not sure how long it took me to realize that if I had a question about repeating expansions made of 1s and 2s, there simply weren't that many to consider. Eureka! Afterward, I wrote a little program to search for expansions with M < 3, and here's what it found.

u	v	w
1	1	1		[1,1]
2	1	1		[2,2]
5	2	1		[2,2,1,1]
13	5	1		[2,2,1,1,1,1]
34	13	1		[2,2,1,1,1,1,1,1]
89	34	1		[2,2,1,1,1,1,1,1,1,1]
233	89	1		[2,2,1,1,1,1,1,1,1,1,1,1]
610	233	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1]
1597	610	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
4181	1597	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
10946	4181	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
28657	10946	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
75025	28657	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
196418	75025	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
514229	196418	1		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
426389	610	233		[2,2,1,1,1,1,1,1,1,1,1,1,1,1,2,2,1,1,1,1,1,1,1,1,1,1]
62210	233	89		[2,2,1,1,1,1,1,1,1,1,1,1,2,2,1,1,1,1,1,1,1,1]
9077	89	34		[2,2,1,1,1,1,1,1,1,1,2,2,1,1,1,1,1,1]
925765	9077	34		[2,2,1,1,1,1,1,1,1,1,2,2,1,1,1,1,1,1,2,2,1,1,1,1,1,1]
1325	34	13		[2,2,1,1,1,1,1,1,2,2,1,1,1,1]
51641	1325	13		[2,2,1,1,1,1,1,1,2,2,1,1,1,1,2,2,1,1,1,1]
135137	1325	34		[2,2,1,1,1,1,1,1,2,2,1,1,1,1,2,2,1,1,1,1,1,1]
194	13	5		[2,2,1,1,1,1,2,2,1,1]
2897	194	5		[2,2,1,1,1,1,2,2,1,1,2,2,1,1]
43261	2897	5		[2,2,1,1,1,1,2,2,1,1,2,2,1,1,2,2,1,1]
646018	43261	5		[2,2,1,1,1,1,2,2,1,1,2,2,1,1,2,2,1,1,2,2,1,1]
7561	194	13		[2,2,1,1,1,1,2,2,1,1,2,2,1,1,1,1]
294685	7561	13		[2,2,1,1,1,1,2,2,1,1,2,2,1,1,1,1,2,2,1,1,1,1]
29	5	2		[2,2,1,1,2,2]
169	29	2		[2,2,1,1,2,2,2,2]
985	169	2		[2,2,1,1,2,2,2,2,2,2]
5741	985	2		[2,2,1,1,2,2,2,2,2,2,2,2]
33461	5741	2		[2,2,1,1,2,2,2,2,2,2,2,2,2,2]
195025	33461	2		[2,2,1,1,2,2,2,2,2,2,2,2,2,2,2,2]
499393	985	169		[2,2,1,1,2,2,2,2,2,2,2,2,1,1,2,2,2,2]
14701	169	29		[2,2,1,1,2,2,2,2,2,2,1,1,2,2]
433	29	5		[2,2,1,1,2,2,2,2,1,1]
6466	433	5		[2,2,1,1,2,2,2,2,1,1,2,2,1,1]
96557	6466	5		[2,2,1,1,2,2,2,2,1,1,2,2,1,1,2,2,1,1]
37666	433	29		[2,2,1,1,2,2,2,2,1,1,2,2,1,1,2,2]

The pattern was far nicer than I had imagined.

expansion(u) = expansion(v) & expansion(w)

Here I'm using “&” as a concatenation operator again, although the details are different than in Multiplication and Square Roots.

Naturally I have many things to say about the table and the pattern.

All the repeat lengths are even.

The table is complete up to repeat length 16. Once I had those results, I was able to see the pattern. After that, I checked and added several longer expansions to make the table contain all solutions with u < 10⁶, but it's still not complete even for repeat length 18.

The pattern applies when u ≥ 5. Applied repeatedly, it expresses any expansion as a combination of expansion(1) and expansion(2). That's why all the expansions are made of pairs of 1s and 2s! Or, to put it another way, that's why I had to write expansion(1) and expansion(2) as [1,1] and [2,2]. In any case, the first two rows of the table are special. To indicate that, I added an empty row underneath.

We already know that expansions made of 1s and 2s aren't guaranteed to have M ≤ 3, but here are two more counterexamples.

• The shortest repeating expansion made of 1s and 2s that doesn't work is [2,1] = (root 3) + 1.
• The shortest repeating expansion made of pairs of 1s and 2s that doesn't work is [2,2,2,2,1,1,1,1].

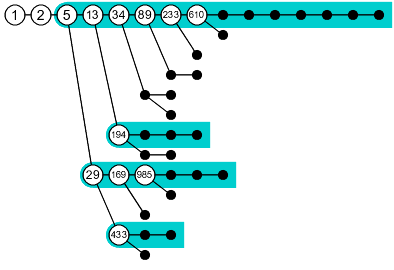
As foretold in The Markov Equation, the order of the rows in the table is determined by that picture of the tree structure. Here's a modified version.

What are the four highlighted things? Well, remember that horizontal lines represent v-flips. One detail I haven't mentioned until now is that in a v-flip, the value of w remains the same, even after normalization. So, in a chain of v-flips, at every step the value of w remains the same, and at every step the same suffix expansion(w) gets appended. The resulting trapezoids in the table are the most visible manifestation of the pattern. To make the four trapezoids corresponding to the four highlighted chains even more visible, I added empty rows around them.

There are seven chains in the picture, four long and three short, but if we look beyond the picture, the entire tree is made of chains. Every w-flip starts a new one, and none of them ever end. The chains just tend to appear short in any finite picture because the value of u grows exponentially along each chain. In fact, at every step the value of u increases by a factor of approximately 3w. That means a factor of 3, 6, or 15 for the long chains, a factor of 39, 87, or 102 for the short chains and three others that are still in the bud, and a factor of 267 or more after that!

Less approximately, the factor is the larger root of the generating function x² − 3wx + 1. The difference is really only noticeable for the long chains, though. In particular, when w = 1 the factor is (R+3)/2, around 2.618, and when w = 2 the factor is 3 + 2 root 2, around 5.828. Even less approximately, the factor isn't constant, but we can write down an exact equation for the value of u if we take into account the smaller root of the generating function. I won't get into how generating functions work, but in a moment I'll show you an example of an exact equation.

You may have noticed that there are two chains with w = 5. Let's call the upper one that starts with 194 chain 5a and the lower one that starts with 433 chain 5b. If we assign sequence numbers to the solutions in chain 5a, like so, …

n	u	v	w
2	194	13	5
3	2897	194	5
4	43261	2897	5
5	646018	43261	5

… then we can do a little algebra and write down that exact equation I was talking about.

u =		[ (1/2) + (11/442) root 221 ] [ (15 + root 221)/2 ]n
	+	[ (1/2) − (11/442) root 221 ] [ (15 − root 221)/2 ]n

What happens if we go backward?

n	u	v	w
5	646018	43261	5
4	43261	2897	5
3	2897	194	5
2	194	13	5
1	13	1	5
0	1	2	5
−1	2	29	5
−2	29	433	5
−3	433	6466	5
−4	6466	96557	5

Surprise, there's chain 5b! That's hard to believe, but fairly easy to explain: the exact equation doesn't know about normalization. To step forward, we do an unnormalized v-flip and then swap u and v, so to step backward, we swap u and v and then do an unnormalized v-flip, and that produces exactly the observed sequence of solutions.

See how the solutions loop around through the tree? At the center of the loop (n = 0) is a solution that when normalized has u = 5, and that shows us the way to the general statement. From any solution, we can do a v-flip and then a w-flip and reach the start of one chain, or we can do two w-flips and reach the start of another chain, and the value of w in those chains is equal to the value of u in the original solution. So, there are two chains per solution … unless the solution is (1,1,1) or (2,1,1), in which case there's only one chain because the initial flips lead to the same place.

By the logic above, we should consider the start of chain 1 to be (5,2,1) … and I do, although that's not the main reason. The main reason is that the first two rows of the table don't fit into the trapezoid for chain 1. To be precise, every row of a trapezoid, even the first, should end with a fresh copy of expansion(w).

I've gotten pretty far off the track of the table and the pattern and onto the track of chains, so I'm sidetracked, or maybe distracted, but here's one more observation about chains that at least takes us back in the right direction.

The denominators (and numerators) of the convergents of the golden mean are Fibonacci numbers. Here's the table from Two Examples with a few additional columns. The numbers in bold are the values of u from chain 1.

		1	1	1	1	1	1	1	1	1	1	1
0	1	1	2	3	5	8	13	21	34	55	89	144
1	0	1	1	2	3	5	8	13	21	34	55	89

The denominators of the convergents of root 2 are Pell numbers. Here's the table from Printer Theory with a few additional columns. The numbers in bold are the values of u from chain 2.

		1	2	2	2	2	2	2	2	2	2	2
0	1	1	3	7	17	41	99	239	577	1393	3363	8119
1	0	1	2	5	12	29	70	169	408	985	2378	5741

That's all on Wikipedia, albeit not all in one place. The article Markov number mentions odd-indexed Fibonacci and Pell numbers, and the other two articles explain the connections to convergents. Here's a new angle, though. The coefficient a₀ doesn't affect the denominators of the convergents, so we can get the denominators that contain chain 2 not just from root 2 but also from 1 + root 2 = [2] = expansion(2), and of course we're already getting the denominators that contain chain 1 from [1] = expansion(1). Does the same relationship hold for any larger numbers? Of course! From [2,2,1,1] = expansion(5) we get denominators that contain chain 5a, …

		2	2	1	1	2	2	1	1	2	2	1	1	2
0	1	2	5	7	12	31	74	105	179	463	1105	1568	2673	6914
1	0	1	2	3	5	13	31	44	75	194	463	657	1120	2897

… and from [2,1,1,2], a rotation of expansion(5) that yields an equivalent number, we get denominators that contain chain 5b.

		2	1	1	2	2	1	1	2	2	1	1	2	2	1	1
0	1	2	3	5	13	31	44	75	194	463	657	1120	2897	6914	9811	16725
1	0	1	1	2	5	12	17	29	75	179	254	433	1120	2673	3793	6466

The relationship also holds for 13 and 29, and that's as far as I've bothered to check. So here's where things stand.

• Does the relationship continue to hold? It seems probable.
• Is the distance between denominators always equal to the repeat length of the expansion? It would be bizarre if it weren't.
• Do the denominators that we get from the unrotated expansion always contain the upper chain of the two? No, in fact the denominators that we get from expansion(29) don't contain either chain.
• Does rotation always produce the desired denominators? Yes, so far, but I wouldn't be surprised if at some point we needed to allow more general equivalent numbers.

That brings me to a big question that I saved for last.

• Does the pattern continue to hold?

The answer has four parts.

• Obviously the experimental evidence is compelling.
• I can't prove it. I gave it a try but didn't get very far.
• I'm certain it can be proved. The article Markov number has a mysterious section about matrices, and that section has one footnote, and that footnote points to the book [Aigner] that I've listed below. When I looked it up on Google Books, as usual I could only see parts of the text, but I could see enough to know that it was exactly the right book. So, I tracked down a physical copy. I still wanted to see how far I could get by myself, so I decided not to read it until I was done writing, but I did peek a little to confirm that it contained at least one proof.
• Thus, the pattern isn't a new result, just a result that's much less well known than it should be.

Here's the book I was talking about. It's around 250 pages, so I don't feel too bad that I couldn't instantly produce a simple proof that the pattern holds.

[Aigner] Markov's Theorem and 100 Years of the Uniqueness Conjecture

Finally, I ought to point out that the notation “expansion(u)” has problems. The obvious problem is that “expansion” is a function of Markov numbers instead of solutions. I specifically said not to do that! Fortunately, the solution is obvious too: make “expansion” be a function of solutions, so that “expansion(u)” becomes “expansion((u,v,w))”. Then the table is a lookup table for that function! However, that leaves us with another problem. Suppose we try to write down the equation for the pattern. The left-hand side is expansion((u,v,w)) and the right-hand side is … what, exactly? How do we find the correct two ancestor solutions? The first one is pretty easy, actually. If we take (u,v,w) and do one u-flip, we get the ancestor that has v in the first position. But, to get the ancestor that has w in the first position, we might need to do any number of u-flips. I don't think there's any way to express that idea without new notation, so I propose an arrow that means “do u-flips until the value in the first position equals the given value”.

expansion((u,v,w)) = expansion((u,v,w) ↓ v) & expansion((u,v,w) ↓ w)

I made a big fat mistake! The values of u in a chain form a sequence. For that sequence, x² − 3wx + 1 is not the generating function, it's the characteristic polynomial of the recurrence relation.

Now I have to write the correct answer on the blackboard. Generating functions and characteristic polynomials are similar in that they both contain a mysterious symbol x. For a characteristic polynomial, the coefficients of the powers of x multiply the terms of the sequence and tell how to construct it, but for a generating function, the coefficients of the powers of x are the terms of the sequence. For the sequence of powers of two, for example, the characteristic polynomial is x − 2, but the generating function is

1 + 2x + 4x² + 8x³ + … = 1/(1 − 2x).

I was tempted to just fix the mistake, but in the end I had to admit that that was forbidden by the rule about persistence of content.