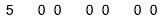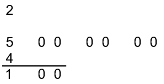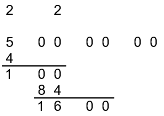Square Roots

To see how it works, let's compute the square root of 5. First we have to write the number as pairs of digits, aligned so that the decimal point falls between pairs and then padded with zero pairs to match the desired precision. So, the following is suitable for computing the square root of 5 or 500, but not 50.

Next, we look at the first pair r and figure out the largest digit d such that d² ≤ r. Here that's 2, since 2² ≤ 5 < 3². Then we write d as the first digit of the answer, and also subtract d² from r and bring the next pair down to join the remainder.

Before we go on, I ought to explain about the concatenation operator “&” that I introduced in Multiplication. In general, to compute c & d, you concatenate the strings of (decimal) digits that represent c and d, so that for example 17 & 29 is 1729. That operation is fairly awkward mathematically, and is best defined only when the arguments are strictly positive. Here, however, the argument d will always be a single digit, so that c & d is just a nice way of writing 10c + d. That operation (“&₁”) makes sense even when the arguments are zero (or negative!).

Now we can do the next step of the calculation. First we take the current answer and double it … that gives us the number 4 that will show up in just a second. Then we look at the current remainder r and figure out the largest digit d such that 4&d × d ≤ r. Here the remainder is 100, so 42×2 = 84 fits, while 43×3 = 129 doesn't, and again we find d = 2. Then we write d as the next digit of the answer, subtract 4&d × d from r, and bring the next pair down to join the remainder.

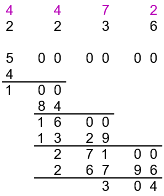
Now I hope you can see where this is going. At each step, we look at the current answer a and remainder r and figure out the largest digit d such that 2a&d × d ≤ r, then we write d as the next digit of the answer, subtract the product from r, and bring the next pair down to join the remainder. Here's how the next two steps turn out; the numbers 1329 and 26796 are 443×3 and 4466×6, respectively.

It's convenient to keep track of the doubled answer above the regular answer, as I've done here in purple.

If you're planning to compute a lot of digits, it's also convenient to write out the multiples of the doubled answer once you've got the first two or three digits. At that point, the “d” in “2a&d” doesn't have much effect on the product value, so given a remainder you can just read off the next digit from the table of multiples. You don't need to keep the table up to date, either. (The idea of writing out multiples also appears in Fractions.)

Another thing you'll notice if you compute a lot of digits is that the length of the remainder tends to grow linearly, so that the calculation becomes more and more tedious. (In fact, the effort required to obtain n digits grows as n².) The small remainder 304, above, simply reflects the fact that the next digit of the expansion happens to be zero.

Or, to put it another way, the small remainder reflects the fact that the answer is an unusually good approximation to the square root of 5. Let's write it out: 2.236² = 4.999696. The difference from 5 is exactly the remainder; that gives you a way to check your arithmetic at the end.

This algorithm is one more example of a little program you can run, by the way.