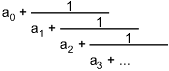Continued Fractions

First I ought to show you what a continued fraction looks like.

The coefficients a_i are positive integers, except for a₀, which can be zero (or maybe negative, but that's not a case I care about). Once you get tired of writing the fractions out like that, you can use the following shorthand, which is standard.

[a₀, a₁, a₂, a₃, … ]

After that, all you need to know is two little algorithms. One takes a number and expands it as a continued fraction; the other takes a continued fraction expansion and produces a sequence of good rational approximations to the original number.

To understand the first algorithm, look back at the picture above. The continued fraction can be thought of as having two parts: an integer part (the coefficient a₀) and a fractional part (everything else). So, if we want to write some number u as a continued fraction, a₀ must equal the integer part of u, and the rest must equal the fractional part of u. But now, if we take the reciprocals of the leftovers, we're right back where we started, with a number and a continued fraction expansion … only now the expansion starts with a₁ instead of a₀. So, we can read off a₁ as the integer part of that number, and so on.

In short, to find the continued fraction expansion of a number u, take the integer part as a coefficient, take the reciprocal of what's left, and repeat. For example, here are the first few iterations for π.

	ai	rest
3.14159	3	0.14159
7.06251	7	0.06251
15.9966	15	0.99659
1.00342	1	0.00342
292.635	292	0.63459

(The values above are correctly-rounded forms of the true values, but if you want to do the calculation yourself, you'll need to keep more digits than I've shown.)

If the number u is rational, the expansion will terminate. For example,

			ai	rest
1309	/	2387	0	1309	/	2387
2387	/	1309	1	1078	/	1309
1309	/	1078	1	231	/	1078
1078	/	231	4	154	/	231
231	/	154	1	77	/	154
154	/	77	2	0	.

So, 1309/2387 = [0,1,1,4,1,2]. And, if you tidy up a little by removing the denominators in the last column, you can see that the continued fraction coefficients are exactly the useless quotients from the Euclidean algorithm!

And, if the number u is algebraic, you can do the calculation symbolically. Here's how it works for the square root of 3 (which I'll call R for short); all you need to know is that R is approximately 1.7, and that you can take reciprocals with just a little algebra, like so.

1 / (R−1) = (R+1) / (R+1)(R−1) = (R+1) / (R²−1) = (R+1) / 2

Here are the first few iterations.

	ai	rest
R	1	R−1
(R+1)/2	1	(R−1)/2
R+1	2	R−1

But then, we've already seen the remainder R−1, so at that point the expansion must repeat! In other words, the expansion of root 3 is [1,1,2,1,2,1,2, … ].

I said I wasn't going to get into any of the theory, but there's one thing that's too interesting not to mention: the expansion repeats if and only if the original number was the root of a quadratic equation … technically, an irreducible quadratic with rational coefficients.

So much for the first algorithm; now, what about the second?

I don't know any easy way to understand the second algorithm, so I'm just going to tell you how to execute it. First, make room for three rows of numbers. In the first row, skip two spaces, then write down the coefficients of the continued fraction you're interested in. In the other two rows, write down the fixed numbers shown below.

		3	7	15	1	292
0	1
1	0

Then, working left to right, fill in the rest of the other two rows using the rule Z = aX + Y, where a is the corresponding expansion coefficient and X and Y are the previous numbers in the same row.

		a
Y	X	Z

Here's how the one above turns out. The number 106, for example, is 15×7 + 1.

		3	7	15	1	292
0	1	3	22	333	355	103993
1	0	1	7	106	113	33102

Now you can read off the sequence of good approximations … in this case, 3/1, 22/7, 333/106, 355/113, and so on. The numbers produced in this way are called convergents. You can also think of convergents as truncated expansions; for example, 333/106 = [3,7,15].

The phrase “good approximation” sounds pretty vague, but here it means something specific. A rational number is a good approximation to a number u if no rational number with the same or smaller denominator is closer to u. All convergents (except sometimes the first) are good approximations in that sense.

However, not all good approximations are convergents. I didn't know much about any other good approximations until recently, when I stumbled across item 101A in HAKMEM. That item points out that one can obtain other good approximations by varying the last coefficient in a truncated expansion. My calculations suggest that if the last coefficient is n, you get good approximations between n/2 and n … although one or both ends may increase by 1, depending on circumstances. I can't guarantee that those values work, or that all good approximations are of that form, but I can show that other values don't work.

Just as an example, the next good approximation to π after 355/113 is [3,7,15,1,146] = 52163/16604.

Finally, I ought to admit I'm using some nonstandard terminology here. A rational number p/q is a good approximation to u if it's the best approximation with denominator not exceeding q. For that reason, people like to say “best” instead of “good”; but then when q varies they're forced to say stupid things like “a best approximation”. Don't do that! (See also Everything Is Best in Favorite Koans.)