Home
> urticator.net
Search
About This Site
> Domains
Glue
Stories
Computers
Driving
Games
Humor
Law
> Math
Numbers
Science
Continued Fractions
Game Theory (Section)
Group Theory
Probability
> Miscellaneous
Commutative Diagrams
On Rectangular Tilings
The Euclidean Algorithm
The Twelve-Note Scale
Tesseract Model
|
> The Pentagon Knot |
The Pentagon Knot
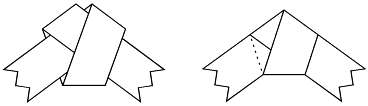
If you take a strip of paper, tie it in a simple knot, and pull it as tight as you can without deforming the paper, you get … a perfect regular pentagon!
I didn't know for sure that the pentagon was regular until just now, when I worked out the geometry of the left-hand figure. It's a nice little math problem, actually. I started from the loose end on the left and used the tilt angle, fold angle, and distance from the vertical axis as parameters, but I'm sure there are better ways to think about it. In fact, there's one below!
Anyway, math or no math, isn't it amazing that it's so easy to construct a regular pentagon? Something like that ought to be common knowledge, but I don't think I've ever seen it written down anywhere.
Another fun thing is, if you use a nice long strip of paper, you can tie five knots in it and make a larger pentagon with knots at the corners.
Now, here's a more general argument that's also a better way to think about the original problem. Suppose we have a regular n-gon and we want one of the edges to be a fold in a strip of paper. If the strip comes in from an edge k steps away, it has to go out to the edge k steps away on the other side, otherwise the fold will be rotated with respect to the edge. And, if we look at any other edge that has a fold, the value of k must be the same, since the fold width varies monotonically with angle. Thus, the figures that can be constructed by folding a strip of paper along the edges of a regular polygon can be classified into a small number of classes [n,k]. Here n is at least 3 and k ranges from 1 up to but not including n/2.
The figures can be classified further according to the number of folds, into classes [n,k,f] let's say, but there are really only three cases of interest. We can make all possible folds and tape the figure into a loop, we can omit one fold and have the ends of the strip exit along a single edge, or we can omit two folds and have the ends exit along two edges k steps apart. The last case includes the pentagon knot (class [5,2,3]), while the first includes the simplest hexaflexagon (class [6,2,3]).
Here are a few points that I like enough to mention but not enough to discuss in any detail.
- The different values of k are like different gears in a Spirograph.
- If n and k have a common divisor, the figure will form a loop before all the edges are used. The maximum number of folds is n/(n,k), where (n,k) is the greatest common divisor of the numbers.
- On the other hand, if the edges aren't all used, it's possible to braid multiple strips together. The maximum number of strips is (n,k).
- In some cases it's possible to braid strips with different values of k.
- In general, the segments of the strip(s) can cross over and under one another in all kinds of crazy ways. This isn't apparent when k = (n−1)/2 (or n/2, see below) because the segments are put into a definite order by the fact that they all pass through the center point of the polygon.
- For f = 1 the classification is ambiguous, but for all other values of f it's well defined.
- The case k = n/2 is degenerate, but with multiple strips it makes sense to allow it. We could let k range up to n−1 or even take any value not divisible by n, but then the classification would be ambiguous again.
The thing that's most pleasing to me about the pentagon knot is how every fold (except one) wraps snugly around another segment of the strip. When else does that happen? Well, to get the snug wrapping part we need k = 2, and then to get a single strip we need n odd, and that does it. For me that's the best generalization of the original idea. The figures are tough to fold, but if you do fold one, you get something like a flattened circle of twisted-pair cable.
On a less serious note, you know how when you go to a restaurant, the straws come in white paper wrappers? I'm pretty sure the only reason I know about the pentagon knot is that I used to fool around with those wrappers when I was a kid. If you take one off carefully, it's natural to smooth it out, and then what can you do? Roll it up, maybe roll it around the straw, fold it into equilateral triangles, or tie it in a knot. Of course you can also leave the wrapper on the straw, tear off one end, and blow into the straw to shoot the wrapper across the room.
Or, do you know this one? If you hold the wrapped straw on end on the table, you can scrunch the wrapper down to the bottom, push it off, then apply a few drops of water to make it wiggle around. Everyone knows how to pick up water with a straw, right?
My parents used to take us kids to all kinds of restaurants, but for some reason in this context I always think of Pizza Hut. How those have changed! They used to be dimly lit and have candles (or oil lamps?) on all the tables in faceted red glass holders, and sometimes they'd have a two-player tabletop arcade game sitting around somewhere, Pac-Man or Galaxian or whatever. And there was none of this modern nonsense about thick and thin crusts, either! Just a nice pepperoni pizza, say, probably with the pepperoni a little charred, with a little red pepper from that glass shaker. Mmm!
So that's what I know about the pentagon knot.
See Also
@ February (2011)