Stable States

So, what was I fiddling around with? I'd been considering the three strategies TT, AC, and AD, remember, and I'd already worked out which of the strategies were stable (with respect to the others); what I wanted to do next was work out which states, or populations, were stable.

First I had to think about how to recognize stable states. Suppose, for example, that the population is a 2:1 mixture of TT and AC. Will that state be stable if the TTers make twice as many points per round as the ACers? It will not! The ACers, collecting fewer resources than the TTers, won't be able to support as many children, and the population balance will change over time. To put it another way, if the total population isn't constrained, the number of points per round a strategy collects is an exponent for exponential growth, and any strategy with a larger exponent will eventually dominate. Thus, the condition for stability is that all strategies present in the population must make the same number of points per round, with all other strategies making the same or less.

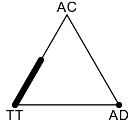
Once you know that, the rest is pretty easy, so I'll skip the details. Here's the final result, the set of stable states plotted in population space.

The point in the lower right represents a population of pure AD, which we've seen is unstably neutral to invasion by TT, while the point in the lower left represents pure TT, which is genuinely neutral to invasion by AC—hence the line of stable states leading away from it.