The Shape of Strategy Space

I think the best way to begin is by restating some generalities about game theory. First, as part of the definition of a game, each player (or role, if you like) is given a certain set of options. Second, to actually play the game, the players occupying the roles must each choose exactly one of the options available to them.

A strategy, then, is a method for choosing an option. That may sound complicated, but at this level of generality it's not—a game consists of making a single choice, no more, so a strategy is just a set of weights for a random choice. By the way, if one of the weights is unity, the strategy is said to be pure; otherwise, mixed. The pure strategies are in one-to-one correspondence with the options, but I think it's correct to consider them to be different things.

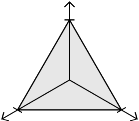
If, for example, one of the players has three options, then a strategy for that player is a set of three weights, i.e., three nonnegative numbers summing to unity. You can think of these numbers as coordinates, like so.

As you can see, the set of possible strategies forms an equilateral triangle. That's strategy space. (It becomes hard to visualize when there are more than four options, of course.)

The same reasoning applies to iterated games, as long as one keeps in mind that each option represents an entire series of decisions. The series of decisions can be contingent on the other players' previous behavior, but it can't include randomness—in the iterated prisoner's dilemma, for example, “tit for tat” is both an option and a pure strategy, but choosing randomly whether to cooperate or defect in each round is a mixed strategy.

In retrospect, I don't think “strategy” was quite the right word to use in the following sentences from The Prisoner's Dilemma.

If the game is repeated (iterated), game theory can properly only be applied to the series as a whole. Each player, instead of choosing whether to cooperate or defect, chooses an entire strategy for when to cooperate and defect.

It is technically true that each player chooses a strategy, but the entireness has more to do with the options than with the strategies (as in “entire series of decisions”, above).

I don't have anything else to say about strategy space. I do, however, have a few things to say about population space, which, unfortunately, I referred to as strategy space in Evolutionarily Stable Strategies.

If we like, we can describe this population as a vector in strategy space,

p AC + (1−p) AD.

The two spaces are so different that I hardly know where to begin. How about this? For any strategy, that is, for any point in strategy space, we can imagine an entire population that uses exactly that strategy, and no other. These pure populations, which correspond to strategies, can then be combined to produce mixed populations, just as pure strategies, which correspond to options, can be combined to produce mixed strategies. So, population space has the same kind of triangular shape as strategy space, but with a monstrously larger number of dimensions.

To put it another way, a pure population of a single mixed strategy is not at all the same thing as a mixed population of pure strategies. For example,

[p AC + (1−p) AD] ≠ p [AC] + (1−p) [AD],

where the symbol [s] denotes a pure population of strategy s. (Does the above remind anyone else of quantum mechanics, or is it just me?)

My only excuse for getting the two spaces confused is that if you happen to be considering populations that contain only a small number of strategies, and if all of the strategies happen to be pure, well, the two do sort of look the same.

Finally, a few remarks about evolutionarily stable (ES) states are in order. First, in this context, “state” is a synonym for “population”. In fact, if you're thinking about the dynamics of populations, the name “state space” agrees with standard mathematical usage. Second, states, or populations, are really the only things that are capable of being ES. The only reason it makes sense to speak of ES strategies is that strategies are in one-to-one correspondence with pure populations.