Polytope Library

So, you can think of this page as a continuation of Contributed Examples. You can also think of it as a continuation of Shape Reference.

I have more to say about the polytopes, but if you'd rather just jump in and start looking at them, here's some quick advice.

• The files are in the subdirectories of the "poly" directory.
• The largest file takes about 15 seconds to load on my computer, but once it's loaded, it runs just fine. So, don't be surprised if there's a delay. On the other hand, my computer is seven years old.
• I recommend using either texture 8 or texture 0.
• When you pick up a shape, the game will draw some marks to show that the shape is selected. You can use control-H to hide the marks if they're in the way.
• You might want to increase the rotate time (on the Motion tab) so that the shapes don't turn as fast.
• If a shape collides with the floor while you're turning it, you can either lift it up a bit or use control-S to turn separation off.
• If you want to understand how the faces of a four-dimensional shape are connected, here's something fun you can do: press control-N to turn X-ray vision on, press control-S to turn separation off, and then fly to the center of the shape and have a look around.
• The paint command "P" is very helpful for picking out individual faces. You can use the same command again to unpaint. You can also use shift-P to change the paint color.

Next, here's what the subdirectory names mean.

• reg3 and reg4 contain regular polytopes. These are the most symmetrical shapes. There are five regular polyhedra and six regular polychora. (Note: the 5-cell is the pentachoron and the 16-cell is the hexadecachoron.)
• uni3 and uni4 contain uniform polytopes. These can have faces of different types but are still very symmetrical. There are 13 uniform polyhedra and 41 uniform polychora, not counting the prismatic ones below.
• uni3p and uni4p contain prismatic uniform polytopes … but only a few of them, because they tend to come in infinite families. In 3D there are prisms and antiprisms of polygons. In 4D there are prisms of prisms, prisms of antiprisms, and a finite number (18) of prisms of the polyhedra from "reg3" and "uni3". The prisms of prisms are actually a subset of the two-parameter family of duoprisms; see the "geom3-torus" section in Geometry Examples #3 for more about that.

  To be uniform, a polytope must among other things have edges that are all the same length. As a result, most of the prismatic polytopes are fairly flat. The octagonal prism is a simple example of this.

• crf3 and crf4 contain Convex Regular-Faced polytopes. In 3D these are known as Johnson solids, and there are 92 of them. The standard names are J1 through J92, I've just added a zero here so the files will sort correctly. In 4D the exact number of CRF polychora is not yet known!

Finally, I'd like to tell you about truncation and all the other crazy operations that you'll see mentioned in the "uni4" directory. Let's start with an easy example, the truncation of a cube in 3D.

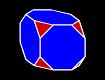
Imagine a cube, and imagine eight diagonal planes just touching the corners of the cube. Now we're going to bring those planes gradually inward. First they just cut off the corners of the cube, leaving little triangles. As we move them further inward, the original square faces of the cube become more and more octagonal, until at a certain point they become regular octagons. That shape is called a truncated cube.

As we go further, the octagons change back into squares (in a different orientation), and the triangular faces touch at the corners. That shape is called a rectified cube, or cuboctahedron.

Although the triangles are touching, we can continue to bring the planes inward, and that turns the triangles into hexagons, and eventually into regular hexagons. That shape is called a truncated octahedron.

Then, finally, the planes reach the centers of the original square faces, and we're left with an octahedron, the dual of the cube. There's no point in moving the planes any further, as it would just make the octahedron smaller.

So, that's the process of truncation, which produces not only truncated shapes but also rectified and dual ones. The word "truncate" is thus slightly ambiguous, but once you understand the process, you should be able to make sense of everything.

Now let's go back and look at the same thing in a different way. Imagine a cube again, and imagine a triangle that connects a corner, an edge midpoint, and a face center. Let's number the vertices of that triangle: 0 for the corner because it's 0-dimensional, 1 for the edge midpoint because edges are 1-dimensional, and 2 for the face center because faces are 2-dimensional. Now I want to make a diagram out of those vertices. The idea is that it's 0-1-2, but because the numbers will always be in the same order, I'll just leave them out and use dots instead: o-o-o.

So far so good? Now imagine all the other similar triangles on the cube. There are eight per face, and six faces per cube, for a total of 48 triangles. If we put big black dots on all the 0-vertices, we get a cube shape. What diagram should we use to represent that shape? Well, we could put a big black dot on the 0-vertex: @-o-o. In the same way, we can draw diagrams for other shapes.

o-o-@ : If we put dots on all the 2-vertices (face centers) and connect them up, we get an octahedron.

o-@-o : If we put dots on all the 1-vertices (edge midpoints) and connect them up, we get a cuboctahedron.

@-@-o : Here the meaning of the diagram is a bit different. If we put dots the correct distance along the lines between the 0-vertices and the 1-vertices, we get a truncated cube.

o-@-@ : Similarly, if we put dots the correct distance along the lines between the 1-vertices and the 2-vertices, we get a truncated octahedron.

So, every shape we could produce by truncation, we can produce by drawing a diagram. The reverse isn't true, though! There are a couple of shapes that we can only produce by drawing a diagram.

@-o-@ : If we put dots the correct distance along the lines between the 0-vertices and the 2-vertices, we get a shape made of triangles and squares. It's called a rhombicuboctahedron.

@-@-@ : If we put dots at just the right place in the middle of the triangles, we get a shape made of hexagons, squares, and octagons. It's called a great rhombicuboctahedron.

There are even a few shapes of interest that can't be produced by drawing a diagram: in 3D, the snub cube and snub dodecahedron, and in 4D, the snub 24-cell and grand antiprism. I'll let you read about those on Teoh's site.

Now let's stop and make a table of what we've learned about diagrams and operations in 3D. The first three can be produced by truncation.

@-o-o : the original shape
@-@-o : truncated
o-@-o : rectified

@-o-@ : cantellated
@-@-@ : omnitruncated

We don't need to include o-o-@ because that's the dual shape, and we don't need to include o-@-@ because that's the truncated form of the dual shape. Does that mean that taking the dual is another operation, one that flips diagrams from left to right? Not exactly. Taking the dual is an operation that you can perform on any shape, but it doesn't just flip diagrams. For example, the dual of the cuboctahedron (o-@-o) is the rhombic dodecahedron, a nice shape but not one we're talking about here. The operation that flips diagrams is taking the dual of the original shape.

What about 4D? Well, you can do exactly the same thing there. Instead of a triangle with three vertices, you have to imagine a kind of right-angled tetrahedron with four vertices, and so on, and here's the result. The first four can be produced by truncation.

@-o-o-o : the original shape
@-@-o-o : truncated
o-@-o-o : rectified
o-@-@-o : bitruncated

@-o-o-@ : runcinated
@-o-@-o : cantellated
@-@-o-@ : runcitruncated
@-@-@-o : cantitruncated
@-@-@-@ : omnitruncated

The words "rectified" and "cantellated" are troublesome in the same way that "face" is. When we talk about faces in 3D, we mean two-dimensional bounding elements, but in 4D the bounding elements and the two-dimensional elements are different things, so part of the meaning gets lost. In the same way, when we move from 3D to 4D, part of the meaning of "cantellated" goes to @-o-@-o and part goes to @-o-o-@.

By the way, my current favorite uniform polychoron is the bitruncated tesseract. The truncation process has reduced the eight cubic faces of the tesseract to truncated octahedra, but they're all still in solid contact with each other via their square subfaces. At the same time, the sixteen new faces produced by truncation, originally tetrahedra, have come into solid contact with each other and are now truncated tetrahedra! It's very 4D.

That's about all I wanted to say about truncation and other operations. It's a reasonable self-contained explanation, but in case you want to do further reading elsewhere, here's some information that should help get you going.

• The diagrams are essentially Coxeter diagrams, I just left out some numbers that tell the exact shape of the triangle or tetrahedron.
• The method of constructing shapes from diagrams is called Wythoff's construction.
• Returning to the cube example, suppose we inflate the cube into a sphere. The triangle becomes a spherical triangle. We can then draw three planes that pass through the center of the sphere and the sides of the triangle. The dots in the Coxeter diagram represent those planes, which are planes of mirror symmetry.
• The 0-dot represents the plane that doesn't pass through the 0-vertex, and so on.
• For every pair of dots, the angle between the associated planes determines whether we draw a line between the dots and whether we put a number under it.

  angle	180/angle	diagram
  90	2	no line
  60	3	no number
  45	4	number 4
  36	5	number 5

• The same numbers are used to make Schläfli symbols. They're basically equivalent to diagrams, just easier to write down.

  {3,3}	tetrahedron
  {4,3}	cube
  {3,4}	octahedron
  {5,3}	dodecahedron
  {3,5}	icosahedron

As one idea for further reading, the Wikipedia page about Schläfli symbols (here) has some nice tables of all these operations (about halfway down).