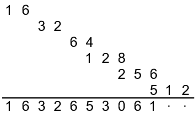Other Denominators

Before we move on to other things, there are some other special denominators that are worth mentioning. Unlike the ones above, which are actually useful, these are mostly just amusing … but that's never stopped me from talking about anything.

If you have a fraction with denominator 10^k+1, you can draw inspiration from the lovely identity

x²−1 = (x+1)(x−1)

and multiply by 10^k−1 to get 10^2k−1. For example,

3/1001 = 2997/999999 = 0.002997002997 … .

That number 2997 may strike you as fishy, and well it should. You can think of it as just being the sort of thing you get when you multiply by 999,

3 × 999 = 3 × (1000 − 1) = 3000 − 3,

but really there is something more sinister going on. To see it, maybe it will help to look at another fraction.

3/999 = 0.003003003003 …

That, of course, can be written as a geometric series that starts with 0.003 + 0.000003; in just the same way, 3/1001 can be written as a geometric series that starts with 0.003 − 0.000003. In other words, it's the same series, but with alternating signs.

Let me go ahead and jump to the general rule. If you have a fraction m/n where the denominator n is close to 10^k, say n = 10^k−d, you can easily write it as a geometric series: just divide the numerator and denominator by 10^k and read off the parameters by comparing to a/(1−r). The first term a is m/10^k, and the ratio r is d/10^k.

So, we've seen d = 1, which gave the original special denominators, and we've seen an example of d = −1, which gave alternating signs, so now let's look at an example of a really interesting one, d = 2. For the one I have in mind, 1/98, the ratio is 2/100, so we ought to see some powers of two, and indeed we do.

1/98 = 0.0102040816326530612244897959183673469387755

Even after the powers of two start to overlap, you can kind of make sense of it for a while, but then it all starts to blur together, for me anyway.

But, if you keep at it, keep adding up the shifted powers of two, guess what? The answer repeats! How freaky is that?!

What's even more freaky, though, is what happens if you shift by one digit instead of two. The first four powers give you 0.1248; adding in 16 gives 0.12496; adding in 32 gives 0.124992; and so on, all the way to the final answer, 0.1249, or rather 0.125, which of course is just 1/8. Isn't that amazing, that the powers of two interlock in just the right way to add up to an infinite string of nines?

When you move on to larger values of d, thinking of the decimal expansion as a geometric series soon becomes less compelling, as you can see in the following table.

100	0.01
99	0.01
98	0.0102040816326530612244897959183673469387755
97	0.01030927835051546391752577319587 …
	62886597938144329896907216494845 …
	36082474226804123711340206185567
96	0.010416
95	0.0105263157894736842
94	0.01063829787234042553191489361702127659574468085
93	0.010752688172043
92	0.010869565217391304347826
91	0.010989
90	0.01

There are some points to notice, though.

• You can think of 1/100 as a geometric series with d = 0.
• 1/97 is moderately nifty.
• 1/96 is amazing in the same way that 1/8 is.

To finish up, here's one more number that I like a lot. It's closely related to 1/98, of course, but more pleasing to me because of how strange it is that a power of seven should produce all the powers of two. I mean, imagine my disbelief when I first discovered this, working out the digits one by one by long division.

1/49 = 0.020408163265306122448979591836734693877551