Some Quirks of Mine

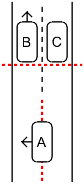
For one thing, when I'm one of several cars passing a slower car, I like to time my lane changes so that I get halfway across just as the car that's currently passing becomes aligned with the slower car. Here's what that looks like when I, as car A, am starting to pass,

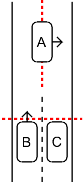
and here's what it looks like when I'm finishing.

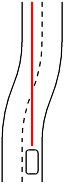
For another thing, when I want to change lanes, if I also happen to be approaching a place where the lanes shift, I like to combine the two, like so.

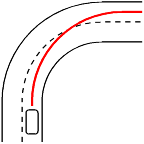
Similarly, if I happen to be approaching a curve, I like to follow a good trajectory that joins the initial and final lanes.

For clarity, I made the trajectory be an arc of a circle, but that's not quite correct. The curvature of a trajectory is essentially proportional to the position of the steering wheel, so on a good trajectory, the curvature shouldn't jump discontinuously from zero to some fixed value, it should change at a comfortable steering-wheel-turning rate.

I can find good trajectories to drive on, but I'm not sure how to describe them mathematically. Should the curvature increase linearly? Should it have a continuous second derivative? Who knows? Actually, civil engineers probably have some idea, since the roads themselves ought to follow good trajectories.

Anyway, returning to the point, I think there is a general principle at work in my quirky lane-changing.

As long as the road isn't straight, you can change lanes along a good trajectory that only curves in one direction.

A straight trajectory, as in the first example, is particularly good.