Positions

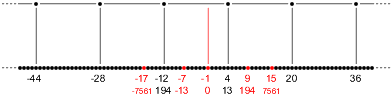
Now let's look at that picture again.

The recurrence relation vastly reduces the amount of experimental evidence we need to show that the picture is valid. Instead of finding an infinite bidirectional chain, or rather finding finite prefixes of the upper and lower chains, confirming that they connect as expected, and then assuming that the rest is there, we just need to find two chain values the right distance apart, and the rest follows. The two values could be the first two values in the upper chain, or they could be the first two values in the lower chain, or they could be … the values v and w right there in the middle! In that case, all the evidence we need is contained in this table from the end of the first part.

	lower		upper
w	L(w)	− 1	L(w)	− 1 − δ	6
v	L(v)	− 1 + δ	L(v)	− 1	10
u	L(u)	− 1	L(u)	− 1	16

The w from the lower denominators and the v from the upper denominators are the right distance apart, thanks to the pattern. (We have to add 2 to account for the center point being −1.)

(L(w) − 1) + (L(v) − 1) + 2 = L(u)

However, since L(w) is even, the position L(w) − 1 is odd, so the corresponding upper denominator is negative and therefore not usable.

The v from the lower denominators and the w from the upper denominators are also the right distance apart.

(L(v) − 1 + δ) + (L(w) − 1 − δ) + 2 = L(u)

And, since δ = ±1, the position L(v) − 1 + δ is even, so the corresponding upper denominator is positive. And there we have it, two chain values the right distance apart! That fits with the picture too, of course.

With that, we've reached the end of the complete thoughts. But, I also have some incomplete thoughts that haven't quite come together yet. They seem more worthwhile than incomplete thoughts usually are, so I'd like to try and present them as well.

First let's look more closely at the table. If we ignore the two δs, then the table says that each value x occurs as a denominator at position L(x) − 1, or equivalently at distance L(x) from the center point −1. That's especially striking for the value u because the expansion coefficients over that distance consist of exactly one iteration of some rotation of expansion(u). Let's make a picture of that that intentionally leaves the rotation unspecified.

If the rotation happened to be the original expansion, then the pattern would apply, …

expansion(u) = expansion(v) & expansion(w)

… and by the logic above, we could easily get a w on the left and a v on the right.

Or, if the rotation happened to be the original expansion rotated by L(v), then the terms would be reversed, …

expansion(w) & expansion(v)

… and we could easily get a v on the left and a w on the right.

Or, best of all, let me remind you of a little fact that I mentioned in Symmetries.

… if we do a u-flip to go backward from (u,v,w), we get either (v,w,x) or (v,x,w), so that the small unit expansion(w) is guaranteed to be either a prefix or a suffix of the large unit expansion(v).

The two possibilities for expansion(v) lead to two possibilities for expansion(u).

expansion(w)	& expansion(x)	& expansion(w)
expansion(x)	& expansion(w)	& expansion(w)

Since the two are rotations of one another, it's completely reasonable to consider only the first possibility. Then we could get the whole table!

In reality, unfortunately, that rotation isn't the one that produces the desired denominators, at least not for u = 7561. But, hey, it's an incomplete thought. The point isn't that it's correct in every detail, the point is that it's plausible. From the fact that some rotation of expansion(u) produces the denominator u at position L(u) − 1, the rest of the table probably follows somehow. So, that fact is the hard kernel at the center of the mystery of chains and denominators.