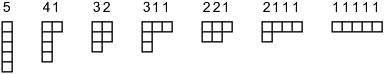Partitions

Since a picture is worth a thousand words, here's a picture of the seven different partitions of 5. The diagrams are called Young diagrams.

Most of the time, the quantity of interest is not any specific partition but rather the number p(n) of different partitions of n.

n	p(n)
0	1
1	1
2	2
3	3
4	5
5	7
6	11
7	15
8	22
9	30
10	42
11	56
12	77

There's no simple formula for p(n), so it's useful to remember the first few values. Under normal circumstances (when I haven't already been thinking about partitions), my limit is probably somewhere around n = 6.

Note that the value p(0) = 1 is not an arbitrary convention. A partition is just a set (multiset) of pieces. It makes sense to talk about the empty set, and in the same way, it makes sense to talk about the empty partition. And, the sum of all the pieces in the empty partition is 0, so the empty partition is a partition of 0. It's also clearly the only one.

Here are two interesting facts about partitions.

First, partitions have duals. To take the dual of a partition, just flip the Young diagram about a line with slope −1. In the picture above, taking duals has the same effect as reversing the order, so that 41 and 2111 are dual, 311 is self-dual, and so on. Unfortunately, the same thing doesn't work in general—taking duals only reverses dictionary order for n ≤ 5.

Second, there's a natural correspondence between the partitions of n and the irreducible representations of the symmetric group S_n. Somehow you can use a Young diagram to actually construct a representation! I've never understood the details, but some day I will, and then I'll write up a nice summary for you.

If you want more facts about partitions, the Wikipedia article has plenty, but to me they're less interesting. I should also point out that with Young diagrams it's conventional to look at the row counts, not the column counts. I'm only breaking the rules here to make the picture more readable.

Although there's no simple formula for p(n), there is an algorithm that's easy to understand, easy to remember, easy to implement in code, and easy to execute by hand. In fact, the algorithm produces a whole grid of meaningful numbers, sort of like the algorithm in Powers of N. The only drawback is that since grids are inherently at least O(n²), it's quite inefficient.

As sometimes happens with math, the key is to make the problem larger. So, let p(n,k) be the number of partitions of n with pieces of size at most k. Here are some sample values from running the algorithm with n = 12.

n	k = 1	2	3	4	5	6	7	8	9	10	11	12
0	1	1	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	2	2	2	2	2	2	2	2	2	2	2
3	1	2	3	3	3	3	3	3	3	3	3	3
4	1	3	4	5	5	5	5	5	5	5	5	5
5	1	3	5	6	7	7	7	7	7	7	7	7
6	1	4	7	9	10	11	11	11	11	11	11	11
7	1	4	8	11	13	14	15	15	15	15	15	15
8	1	5	10	15	18	20	21	22	22	22	22	22
9	1	5	12	18	23	26	28	29	30	30	30	30
10	1	6	14	23	30	35	38	40	41	42	42	42
11	1	6	16	27	37	44	49	52	54	55	56	56
12	1	7	19	34	47	58	65	70	73	75	76	77

How do we know the value of, say, p(12,4)? Well, suppose we have a partition of 12 with pieces of size at most 4. The obvious question to ask is how many pieces of size 4 it has.

• If zero, then the pieces are all actually of size at most 3. There are p(12,3) partitions like that.
• If one, then that covers 4 of the 12 and leaves 8 that need to be covered by pieces of size at most 3. So, there are p(8,3) partitions like that.
• If two, then that covers 8 and leaves 4, so there are p(4,3) partitions like that.
• And, if three, then that covers 12 and leaves nothing, and there's only p(0,3) = 1 partition like that.

To sum up,

p(12,4) = p(12,3) + p(8,3) + p(4,3) + p(0,3),

or in the general case,

p(n,k) = sum _{j=0 … ⌊n/k⌋} ( p(n−jk,k−1) ).

With that equation, we can compute any column from the previous one. Then we need only observe that the first column is all 1s, and we have an algorithm. We can do better, though! Returning to the p(12,4) example, let's also write down the equation for p(8,4).

p(8,4) = p(8,3) + p(4,3) + p(0,3)

If we substitute that into the equation for p(12,4), we find

p(12,4) = p(12,3) + p(8,4),

or in the general case,

p(n,k) = p(n,k−1) + p(n−k,k).

With that equation, too, we can compute any column from the previous one, as long as we compute the cells in an appropriate order, e.g. downward. (How many upward steps can there be?) The advantage is that the cost per cell is fixed. The disadvantage is that the equation has an edge case: when n < k the second term on the right shouldn't even be there (and is undefined).