On Rounding

What do you think of this rule that I used implicitly above?

x and y will round to the same number if and only if |x − y| < 0.5

If x or y is an integer, the rule is almost true, giving the wrong answer only in one of the two edge cases. If x = 2, for example, then y = 1.5 rounds to the same number, but y = 2.5 doesn't.

In general, though, the rule is only a rough approximation to the truth. If x = 1.501, for example, then y = 2.499 at distance 0.998 rounds to the same number, but y = 1.499 at distance 0.002 doesn't. (We ran into the same problem in Exponentials, Continued.)

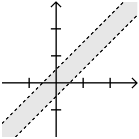
Here's a picture of when |x − y| < 0.5, …

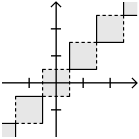
… and here's a picture of when x and y round to the same number.

I think it's fairly standard to use solid lines for closed edges and dashed lines for open edges. In any case, that's what I did here.

The first picture is only an approximation to the second, but it is an approximation, in that it has the same area and is more or less in the right place.

I don't have a strong opinion about how to round negative numbers, but here's what comes to mind.

1. Why would you ever want to do that?
2. You should ignore the minus sign so that round(−x) = −round(x). That's what I did in the second picture. The Wikipedia article on rounding calls that method “round half away from zero”.
3. On the other hand, my experience with the “mod” operation (Reduction Rules) tells me that having a function change behavior at zero is extremely annoying. So, maybe the method “round half up” would be better? Then we'd have round(x + n) = round(x) + n for every integer n.

Now we're equipped to understand the truth about when da and db round to the same number. The second picture shows when x and y round to the same number, so all we have to do is consider the point with coordinates x = da and y = db. As d varies, that point traces out a nearly-diagonal line (slope 0.999875 and a bit), and wherever that line intersects one of the gray squares, the rounded numbers are the same.

• Around d = 0, the numbers are approximately 100% the same.
  • The first difference occurs at d = 0.079365 (da = 0.5).
  • The first difference with integer d occurs at d = 5 (da = 31.5).
• Around d = 635, the numbers are approximately 50% the same.
• Around d = 1270, the numbers are approximately 0% the same.
  • The last time the numbers are the same is in an open interval before d = 1269.920634 (da = 8000.5).