How Many Acknowledgments?

A: When should we meet?

B: Any time is fine, you pick one.

A: OK, I pick 10:00 on Thursday.

B: OK, got it.

A: See you then.

It seems pretty clear to me that B should send that first acknowledgment (“got it”). As part of a conversation, it's courteous, but as part of an email exchange, it's essential, because without it, A would be in limbo, not knowing whether or not the meeting was really set.

I have mixed emotions about the second acknowledgment. On the one hand, it seems kind of excessive; on the other, without it, B would be in limbo, because the first acknowledgment might have gotten lost and left A in limbo. In practice, it isn't necessary, because email rarely gets lost. The first acknowledgment might get delayed, or deleted by a spam filter, but most of the time it will get through; and even if it doesn't, it's not the end of the world, people can always call each other and sort things out.

So, in practice, the second acknowledgment is probably unnecessary, but what about in theory? I like theory too, you know! So, let's consider a formalized version of the problem. Suppose the parties communicate purely by email, and suppose it is the end of the world if the message doesn't get through.

hey gorby!  weve got a bomb test today,
dont nuke us or anything k?  lolz!!  R

How many acknowledgments is enough to make everything perfectly clear?

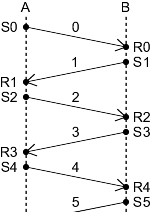
Let's also introduce some notation. Let's count the messages starting with zero, so that message 0 is the original message (the “0riginal”), message 1 is the first acknowledgment, message 2 is the second, and so on; and let's define two events for each message: event Sn, when message n is sent, and event Rn, when it's received. Then the whole exchange looks something like this.

Now all we need to do is decide what the goal is—what counts as “perfectly clear”. Maybe each side should know that the original message was received?

A knows R0
B knows R0

In that case … well, when R0 happens, of course B knows it right away, but A doesn't know it until the first acknowledgment arrives, so the goal is reached when R1 happens. Or maybe each side should know that the original message was received, and that the other side knows it too?

A knows R0
B knows R0
A knows (B knows R0)
B knows (A knows R0)

The first new condition doesn't add anything, but the second one does; we can work out the details with a bit of symbolic calculation.

B knows (A knows R0) = B knows R1 = R2

So, the goal is reached when R2 happens. We've now rehashed my original argument in favor of sending a second acknowledgment: until R2, B doesn't know that A knows R0.

To put it another way, the first set of conditions shows that there's no confusion about R0, while the second set of conditions shows that everyone knows there's no confusion. So, for example, in the interval between R1 and R2, A knows R0 happened, but can claim not to, to be confused; and B can't tell the difference.

Anyway, the more I think about it, the more I like that as a stopping point. We have a decent case in favor of second acknowledgment, and as a bonus we have a definition of “perfectly clear”: a fact is perfectly clear if each side knows it, and knows that the other side knows it.

By the way, we can get the same answer by working backward. Suppose Rn just happened (for n even, let's say). How much of the past is perfectly clear? Well, B knows everything, all the way to the present. A knows everything up to Sn; and B, who knows everything, knows that. And A knows that B knows … what? Well, as far as A knows, B doesn't even know message n−1 arrived, so the last event for B is S(n−1), and that's the most recent perfectly clear event. The event immediately before that is R(n−2); so taking n = 2 we find that R0 is perfectly clear at R2, exactly as expected.

That same result can give us answers to other questions as well. For example, in other circumstances we might want it to be perfectly clear that the original message went through, and that the acknowledgment was received, i.e., that R1 happened. For that, we can set n = 3, and see that R1 is perfectly clear at R3.

I hope that was all fairly easy reading, because it took me a long time to get it right. If you try to think through the problem yourself, you'll see what I mean … it's very easy to become totally confused. But, maybe I can help you avoid the worst pitfalls. There are two invalid arguments that I found very compelling … first I'll present them, then I'll explain what's wrong with them.

• For everyone to be happy, R2 has to occur, right? But, at the moment it occurs, A can't be happy, because ve doesn't even know that anything has happened. So, B needs to send message 3 to tell A about R2. In other words, for everyone to be happy, R3 has to occur. But, at the moment it occurs, B can't be happy, because ve doesn't even know that anything has happened. So, A needs to send message 4 to tell B about R3; and so on.
• Suppose the exchange is finished and everyone is happy, and think about the last message for a second. The sender has no idea if the message even arrived, but is happy nonetheless; it must not matter if the message doesn't arrive. Why even send it, then? Everyone must already be happy. But then, by the same logic, the previous message must also be unnecessary; and so on.

There are several small lessons here.

• The term “happy” is totally undefined. It's easy to confuse yourself if you don't even know what your words mean.
• It's easy to confuse Rn with knowing about Rn. In the first argument, for example, I said A doesn't even know that anything has happened. That's true, but it doesn't matter … we're talking about R2, not about knowing about R2.
• It's important to make precise statements. I claim that if R2 occurs, R0 is perfectly clear. It's true that message 2 is the last message, but a scenario in which it doesn't arrive has no bearing.

That last point leads right into the big lesson. In the protocol I've been talking about, after the original message is sent, each side does nothing unless a message arrives. So, if a message is lost, the exchange grinds to a halt, and R0 never becomes perfectly clear. No number of acknowledgments is enough to recover from that! In other words, if you want to get rid of the condition “if R2 occurs”, you need to add some kind of retransmission to the protocol.

Now, here's the punchline. The protocol I've been talking about may be seriously flawed, but it's still the actual protocol most people use for email! If a message is lost, there's simply no telling how long it will be before someone notices. It might take days or weeks, or it might not happen at all! And, that's true even if the parties exchange messages regularly … depending on the content, a lost message might just never be noticed.

I find that very disturbing, actually, but since I only figured it out as I was writing, I don't really have any further thoughts yet. I mean, I knew email could get lost, but I'd never framed the problem in such a disturbing way. Is there any solution? Certainly I could keep track of my outgoing email until I know it's been received, and retransmit (or call on the phone) as necessary, but that would only solve half the problem … if someone else's email is lost on the way to me, there's nothing I can do about that.

If you'd like to see what a more reliable protocol looks like, check out TCP (Transmission Control Protocol) … it uses both acknowledgment and retransmission. That and IP (Internet Protocol) are what the internet is built on!

This is the Two Generals Problem.